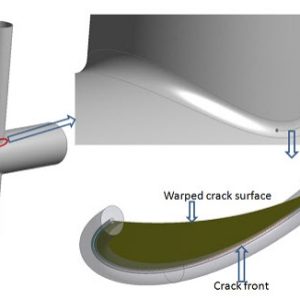
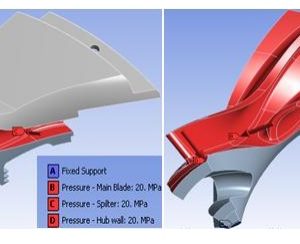
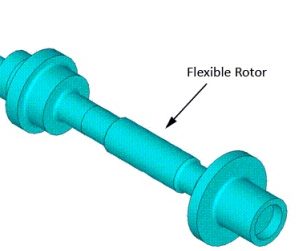
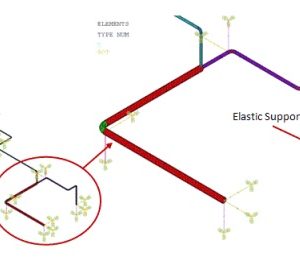
توضیحات
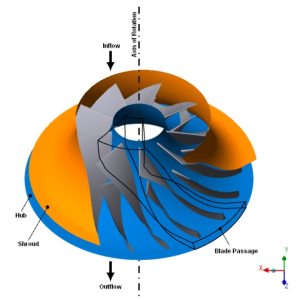
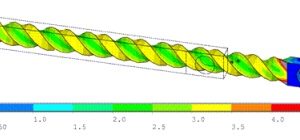
این مسئله ، تجزیه و تحلیل تیغه پروانه گریز از مرکز را با استفاده از روشهای مدلسازی چرخهای و روشهای حل اغتشاش خطی را نشان میدهد. این تحلیل شامل یک تحلیل مودال، یک تحلیل هارمونیک کامل، یک آنالیز مودال پیش تنیده با استفاده از اغتشاش خطی، یک تحلیل هارمونیک کامل پیش تنیده با استفاده از اغتشاش خطی، و یک تحلیل هارمونیک حالت پیش تنیده – برهم نهی با استفاده از اغتشاش خطی است. نتایج تجزیه و تحلیل تقارن چرخه ای به دست آمده از تجزیه و تحلیل مدل کامل (360 درجه) تأیید می شود.
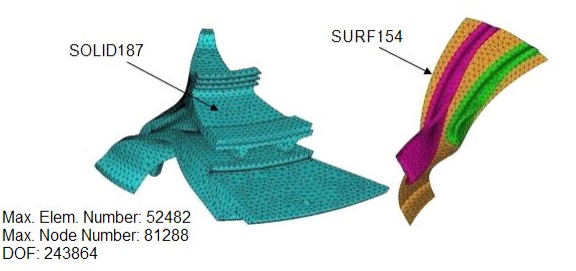
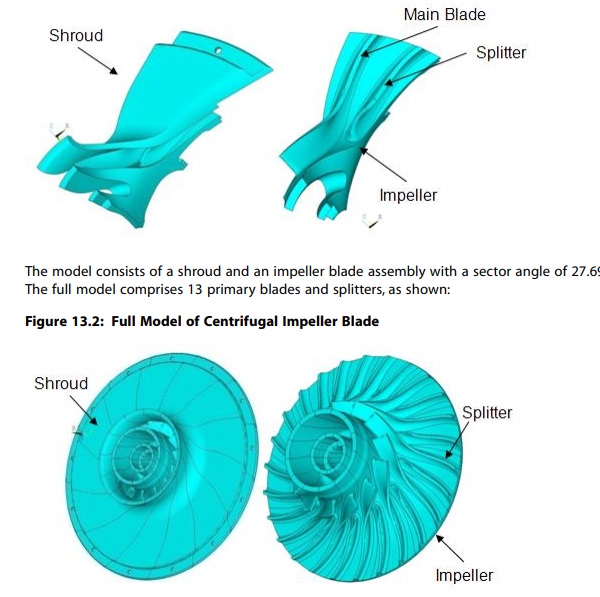
مدلسازی تقارن چرخهای ابزاری قدرتمند برای تحلیل سازههایی با الگوی هندسی تکراری 360 درجه حول یک محور تقارن است. تقارن چرخه ای در بسیاری از سازه های مهندسی عمران مانند گنبدها، برج های خنک کننده و دودکش های صنعتی دیده می شود. همچنین می توان آن را در تجهیزات مکانیکی پیدا کرد.مانند فرز، دیسک پره های توربین، چرخ دنده ها، فن ها و پروانه های پمپ. مدلهای متقارن چرخهای را میتوان با استفاده از یک بخش واحد (به نام بخش اصلی) از کل ساختار حل کرد و شرایط مرزی تداوم و سازگاری بین زیرساختهای چرخهای را اعمال کرد. تجزیه و تحلیل تقارن چرخه ای به میزان زیادی اندازه مدل و هزینه محاسباتی را کاهش می دهد.
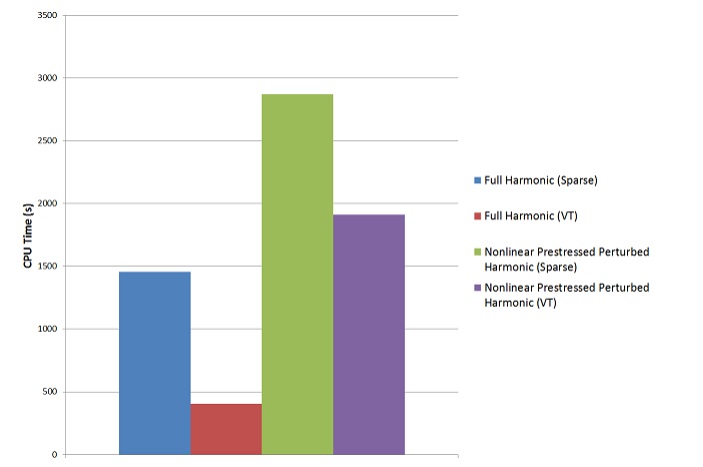
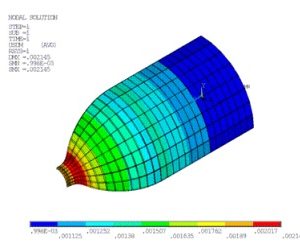
مودال، مودال پیش تنیده آشفته با راه حل استاتیک پایه خطی و غیرخطی، هارمونیک کامل، هارمونیک کامل پیش تنیده آشفته با حل استاتیک پایه غیرخطی، و تحلیل هارمونیک حالت پیش تنیده آشفته با حل استاتیک پایه غیرخطی بر روی مدل بخش چرخه ای انجام می شود.
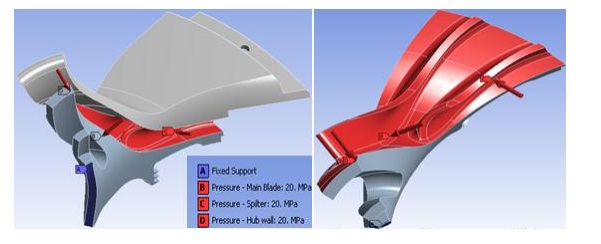
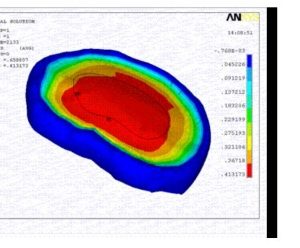
تحلیل تقارن چرخهای مدال آشفته شامل شرایط پیش تنیده اولیه از هر دو تحلیل استاتیکی خطی و غیرخطی است. حالت تنش اولیه با محلول استاتیکی خطی توسط مجموعه پروانه چرخان و همچنین بار فشار اعمال شده بر روی تیغه پروانه ایجاد می شود. اولیه
حالت تنش با تحلیل استاتیکی غیرخطی توسط تیغه پروانه چرخان، بار فشاری اعمال شده بر روی تیغه پروانه و بارگذاری حرارتی اعمال شده بر روی تمام گرههای مدل مونتاژ تیغه پروانه ایجاد میشود. تجزیه و تحلیلهای تقارن چرخهای هارمونیک کامل آشفته و حالت برهمنهاد آشفته شامل شرایط پیش تنیده اولیه به دلیل تحلیل استاتیکی غیرخطی است. حالت تنش اولیه با چرخش مجموعه پروانه و بارگذاری حرارتی اعمال شده بر روی تمام گره های مدل مونتاژ تیغه پروانه ایجاد می شود.
مودال، مودال آشفته، هارمونیک کامل، و هارمونیک کامل آشفته کامل (360 درجه) مدل همچنین برای تأیید صحت نتایج مدل بخش چرخه ای انجام می شود